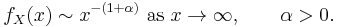Fat-tailed distribution

A fat-tailed distribution is a probability distribution that has the property, along with the heavy-tailed distributions, that they exhibit extremely large skewness or kurtosis. This comparison is often made relative to the ubiquitous normal distribution, which itself is an example of an exceptionally thin tail distribution, or to the exponential distribution. Fat tail distributions have been empirically encountered in a fair number of areas: economics, physics, and earth sciences. Fat tail distributions have power law decay in the tail of the distribution, but do not necessarily follow a power law everywhere.[1]

Contents

Definition

The distribution of a random variable X is said to have a fat tail if

\Pr[X>x] \sim x^{- \alpha}\text{ as }x \to \infty,\qquad \alpha > 0.\,

That is, if X has a probability density function, 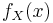f_X(x),

f_X(x) \sim x^{ - (1 %2B \alpha)} \text{ as }x \to \infty, \qquad \alpha > 0.\,

Here the notation "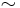 \sim " is the "twiddles" notation used for the asymptotic equivalence of functions. Some reserve the term "fat tail" for distributions only where 0 < α < 2 (i.e. only in cases with infinite variance).

Fat tails and risk estimate distortions

By contrast to fat tail distributions, the normal distribution posits events that deviate from the mean by five or more standard deviations ("5-sigma event") are extremely rare, with 10- or more sigma being practically impossible. On the other hand, fat tail distributions such as the Cauchy distribution (and all other stable distributions with the exception of the normal distribution) are examples of fat tail distributions that have "infinite sigma" (more technically: "the variance does not exist").

Thus when data naturally arise from a fat tail distribution, shoehorning the normal distribution model of risk—and an estimate of the corresponding sigma based necessarily on a finite sample size—would severely understate the true risk. Many—notably Benoît Mandelbrot as well as Nassim Taleb—have noted this shortcoming of the normal distribution model and have proposed that fat tail distributions such as the stable distribution govern asset returns frequently found in finance.[2]

The Black–Scholes model of option pricing is based on a normal distribution. If the distribution is actually a fat-tailed one, then the model will under-price options that are far out of the money, since a 5 or 7 sigma event is much more likely than the normal distribution would predict.

Applications in economics

In finance, fat tails are considered undesirable because of the additional risk they imply. For example, an investment strategy may have an expected return, after one year, that is five times its standard deviation. Assuming a normal distribution, the likelihood of its failure (negative return) is less than one in a million; in practice, it may be higher. Normal distributions that emerge in finance generally do so because the factors influencing an asset's value or price are mathematically "well-behaved", and the central limit theorem provides for such a distribution. However, traumatic "real-world" events (such as an oil shock, a large corporate bankruptcy, or an abrupt change in a political situation) are usually not mathematically well-behaved.

Historical examples include the Black Monday (1987), or the unpegging of some currencies.[3]

Fat tails in market return distributions also have some behavioral origins (investor excessive optimism or pessimism leading to large market moves) and are therefore studied in behavioral finance.

In marketing, the familiar 80-20 rule frequently found (e.g. "20% of customers account for 80% of the revenue") is a manifestation of a fat tail distribution underlying the data.

Applications in geopolitics

In The Fat Tail: The Power of Political Knowledge for Strategic Investing, political scientists Ian Bremmer and Preston Keat propose to apply the fat tail concept to geopolitics. As William Safire notes in his etymology of the term,[4] a fat tail occurs when there is an unexpectedly thick end or “tail” toward the edges of a distribution curve, indicating an irregularly high likelihood of catastrophic events. This represents the risks of a particular event occurring that are so unlikely to happen and difficult to predict that many choose to ignore their possibility. One example that Bremmer and Keat highlight in The Fat Tail is the August 1998 Russian devaluation and debt default. Leading up to this event, economic analysts predicted that Russia would not default because the country had both the ability and willingness to continue to make its payments. However, political analysts argued that Russia’s fragmented leadership and lack of market regulation—along with the fact that several powerful Russian officials would benefit from a default—reduced Russia’s willingness to pay. Since these political factors were missing from the economic models, the economists did not assign the correct probability to a Russian default.

See also

References

  1. ^ http://books.google.com/books?id=A9KumbRohY4C&pg=PA487&dq=%22fat+tail%22&cd=6#v=onepage&q=%22fat%20tail%22&f=false
  2. ^ N.N. Taleb, The Black Swan, Penguin, 2007
  3. ^ http://books.google.com/books?id=jy0WU884hW0C&pg=PA288&dq=%22fat+tail%22&cd=4#v=onepage&q=%22fat%20tail%20event%20in%20the%20real%22&f=false
  4. ^ On Language: Fat Tail

External links